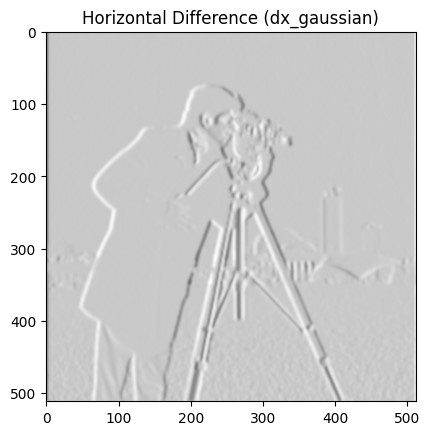
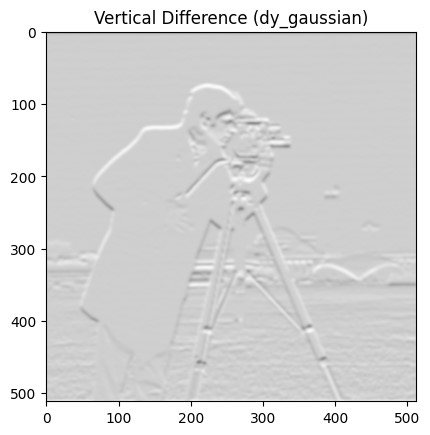
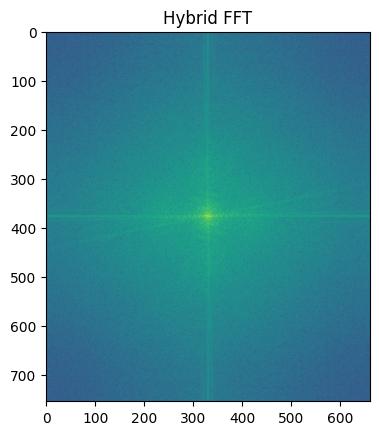
Two finite difference kernels were implemented as NumPy arrays to compute partial derivatives:
dx = np.array([[1, -1]])for horizontal changesdy = np.array([[1], [-1]])for vertical changes
These kernels were applied to the original image using scipy.signal.convolve2d with the parameter mode='same', resulting in two images representing partial derivatives in the x and y directions.
To create a single edge image, the gradient magnitude was calculated at each pixel using:
np.sqrt(dx ** 2 + dy ** 2)This operation effectively computes the L2 norm of the gradient vector formed by corresponding pixel values from the two partial-derivative images, producing the final edge-detected image.
Outputs
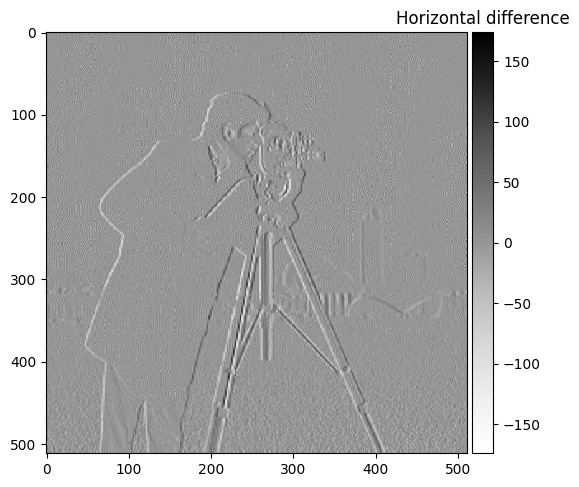
Cameraman (dx)
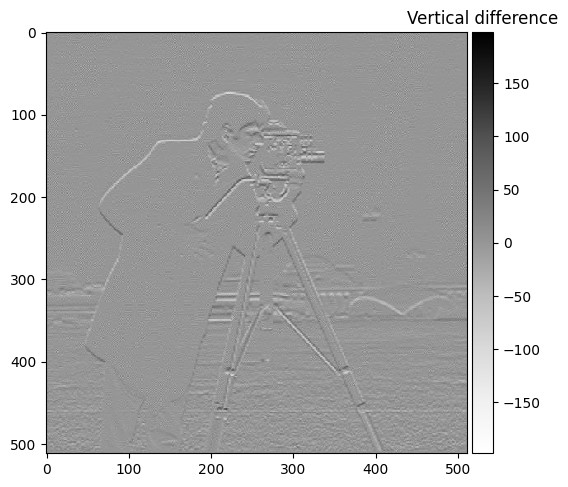
Cameraman (dy)

Cameraman (Gradient, binarized)